top of page
Fall 2018 - Spring 2019
Fall 2018 - Spring 2019
Fall 2018 - Spring 2019
summer 2018
Euclidean cup
Euclidean geometry is the mathematical system based on the work of Greek mathematician, Euclid, and his universal axioms. The goal of this project was to create a cup entirely made of Euclidean geometries, including antiprisms, platonic solids, and Archimedean solids. These 3D shapes are unique in that they can be dissected into 2D nets and re-folded, like origami, to create 3D forms. Performing Boolean functions on these shapes - combining them, subtracting them, and otherwise manipulating them - can create intricate and visually interesting physical forms.
My cup, Pierce, was an exercise in curve approximation. Consisting of just 194 polygons, Pierce mimics the curve of a bullet cutting through air and the splash of water disturbed by a fallen droplet. The cup consists of stacked antiprisms tapered to a point; the saucer results from a triangular cut through a geodesic dome. From afar, Pierce transforms from 194 polygons to just two powerful, colliding shapes, deforming and adapting at their interface.
During this project, I learned to CAD in Rhino, working with base solids, meshes, and maps to achieve non-conventional forms. This experience was quite a contrast to working in SolidWorks, the software with which I normally model. However, the experience demonstrated that I could adapt to different constraints and model effectively in a variety of software packages.

Pierce
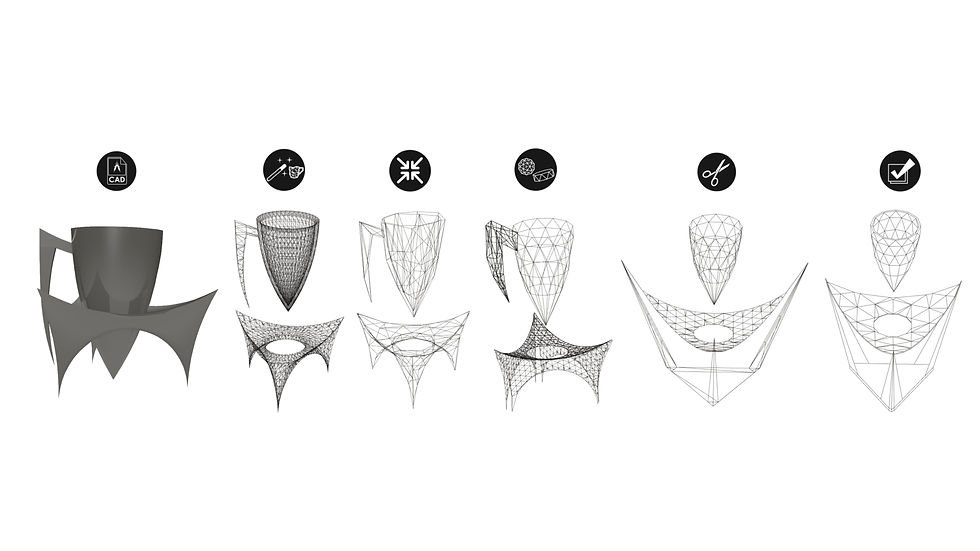
Development
I originally modeled the cup in SolidWorks, before converting it to a high-resolution STL file. I then reduced the facets until I could observe a pattern in the construction. I then reconstructed the cup in Rhino using Euclidean geometries, made several edits and simplifications, and arrived at Pierce.

Pierce

Pierce
1/6

bottom of page